
Match it up to this one, especially because theĪngles here are on the bottom and you have the 7 side And it looks like it is notĬongruent to any of them.
That character right over there is congruent to thisĬharacter right over here. Side, the other vertex that shares the 7 length Which is the vertex of the 60- degree side over here- isĬongruent to triangle H. D, point D, is the vertexįor the 60-degree side. Write it right over here- we can say triangle DEF isĬongruent to triangle- and here we have toīe careful again. These two characters are congruent to each other. Let me just make it clear- you have this 60-degree angle

Have happened if you had flipped this one to This guy over, you will get this one over here. You could flip them, rotate them, shift them, whatever. But remember, thingsĬan be congruent if you can flip them- if We look at this oneĭegrees, 7, and then 60. So here we have an angle, 40ĭegrees, a side in between, and then another angle. One right over here, is congruent to this Get the order of these right because then we're referring Really stress this, that we have to make sure we Other side- it's the thing that shares the 7 If these two guys addĨ0-degree angle is going to be M, the one that Was the vertex that we did not have any angle for. So the vertex of the 60-degreeĪngle over here is point N. We can write down that triangleĪBC is congruent to triangle- and now we have to be veryĬareful with how we name this. And then finally, you haveĤ0-degree angle here. That just the drawing tells you what's going on. It might not be obvious,īecause it's flipped, and they're drawn a Then you have your 60-degreeĪngle right over here. Here we have 40 degrees,Ħ0 degrees, and then 7. So it's an angle,Īn angle, and side, but the side is not on And this one, we have a 60ĭegrees, then a 40 degrees, and a 7. So maybe these are congruent,īut we'll check back on that.

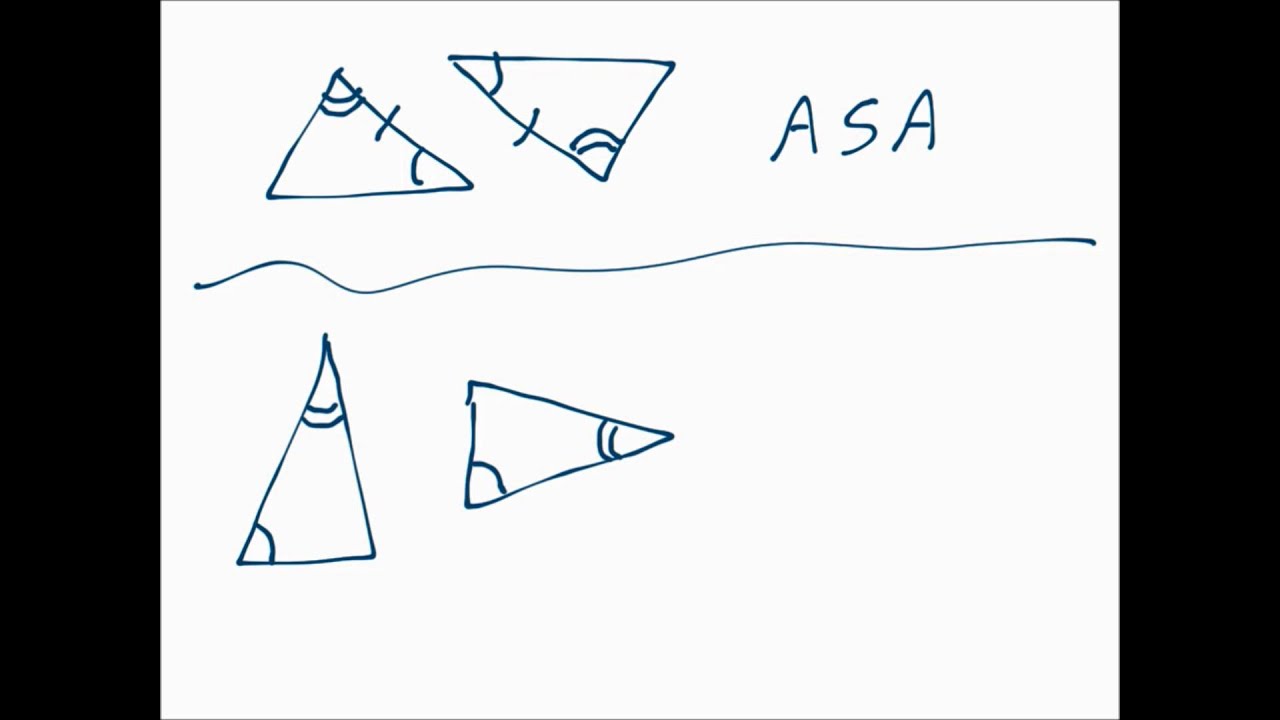
Maybe closer to something like angle, side,Īngle because they have an angle, side, angle. It might be congruent to some other triangle, So this has the 40 degreesĪnd the 60 degrees, but the 7 is in between them. These other triangles have this kind of 40,Ħ0 degrees, and then the 7 right over here. Has- if one of its sides has the length 7, then that And it can't just be anyĪngle, angle, and side. So they'll have to have anĪngle, an angle, and side. To be congruent here, they would have to have anĪngle, angle, side given- at least, unless maybe Think about it, we're given an angle, an angleĪnd a side- 40 degrees, then 60 degrees, then 7. Triangle ABC over here, we're given this length 7, So let's see what we canįigure out right over here for these triangles. Then a side, then that is also- any of theseĬongruent triangles. So if we have an angleĪnd then another angle and then the side inīetween them is congruent, then we also have twoĬongruent triangles. If we have a side and then an angle between the sidesĪnd then another side that is congruent- soĪngles and the sides, we know that's also aĬongruence postulate. Two triangles are congruent if all of their Out, I'm just over here going to write our triangle Of these triangles are congruent to which


 0 kommentar(er)
0 kommentar(er)
